Nakamoto Dollar and The Math Behind Ethena
Breakdown of the Nakamoto Dollar proposal that evolved into Ethena.
NOTE: This post is part 4 of a multi-essay effort to understand Ethena from first principles. Many people have asked me to write a take on Ethena but truth be told I don't know how it works. Each week I will cover a concept that will help me get closer to breaking down the synthetic dollar protocol. This post is focused on Arthur Hayes’ Nakamoto Dollar and Inverse Perps. The previous post in the series is here.
A friend of mine goes skiing to Hokkaido every year.
He explained that the combination of food, culture and the skiing experience is so profound that he vowed to visit at least once every year for the rest of his life.
Arthur Hayes’ own experiences chasing powder in Asia became the title for one of his most impactful posts: Dust on Crust.
This post provided a blueprint for the Ethena stablecoin through its presentation of what Hayes called the “Nakamoto Dollar”.
Its main contribution is the magical math of inverse perpetuals that lends itself to the creation of synthetic assets introduced with a provocative note:
For those of you who do not like maths, please accept my condolences in advance. I promise that when you are done reading this, you can go back to reducing your cognitive abilities watching TikTok thirst traps.
While I can't promise to make the math as exciting as a TikTok, I will certainly make it more visual here.
The Nakamoto Dollar in a Nutshell
The Nakamoto Dollar aims to create a capital efficient synthetic dollar that doesn't rely on the fiat banking system.
Not relying on the fiat banking system immediately rules out fiat-backed stablecoins.
But “capital efficiency” refers to how much liquidity is required to mint 1 USD worth of assets.
A stablecoin like DAI is not reliant on the fiat banking system but is overcollateralized, meaning that you need more than 1 USD worth of crypto to mint 1 DAI.
To create this, Hayes constructs a position denominated entirely in bitcoin that replicates the payoff of 1 USD.
He achieves this with a single trading position.
His key insight is that since perpetuals require margin to be posted, instead of minting 1 USD worth of crypto directly, the aim is for the sum of the posted margin and the value of the perpetual to add up to 1 USD at all times.
Everything you need to know about Perpetuals in 2 minutes
Feel free to skip this if you are already familiar with perpetual swaps.
A perpetual tracks the price of another asset (or some derivative of this value).
Instead of purchasing the asset outright, you post margin, going “long” on the asset with someone else going “short”.
For example, a normal BTCUSD perpetual allows “longs” (traders expecting the Bitcoin price to increase) to speculate on the price of Bitcoin in USD.
If the price of Bitcoin is $1 USD, they can enter into a long position. The value of this long position will always be the current price of Bitcoin minus 1 (the price of Bitcoin at entry). The opposite is true for the shorts.
There is also a margin requirement, for example a 20% margin requirement necessitates that the longs post $0.2 to enter the position.
If the total price of the margin + the perp position value falls below 0, the position would be liquidated. This would happen if the price of Bitcoin fell by more than 20%.
Inverse perps
While the BTCUSD perp tracks the value of 1 BTC in US Dollar terms, an inverse perpetual, well, tracks the inverse.
The short position tracks the value of 1 USD in Bitcoin.
Note: “longs” are not people who are long the tracked asset (USD in this case). Longs are still people that are long on BTC.
Putting it all together
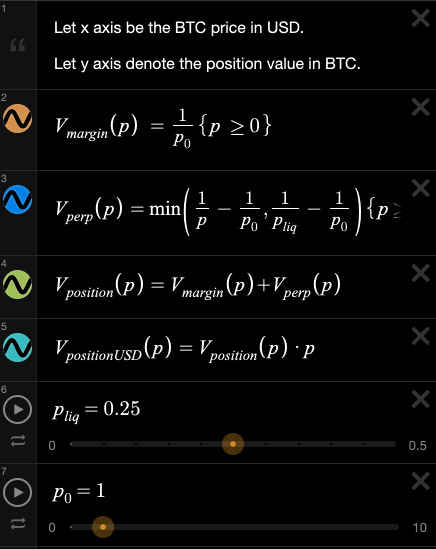
Hayes’ idea is to post 1 USD worth of Bitcoin as margin and use it to open a short position in an inverse perpetual.
First, lets assume the initial price of BTC (p0) is indeed 1 USD.
This means that the margin will be exactly 1 BTC.
The value of our perpetual position is a little bit more complex. The value it is tracking is 1/p where p is the current price of BTC in USD.
The value of going short is the difference of 1/p - 1/p0.
Now the total of these positions evidently is equal to 1/p.
The price of which is exactly 1 USD by definition of p.
The best part?
This position can never get liquidated because it’s value never goes below 0.
Too good to be true?
There is a small problem.
Consider what happens to the longs when the price of BTC drops.
They would effectively have to supply increasing amounts of BTC, an asset of finite supply.
At some point, the longs would get liquidated and the short position would stop increasing in value while the value of our margin would keep dropping.
If the liquidation price p_liq would be 0.25, our total position in BTC terms would be capped at 4 BTC and the USD value of our position would eventually fall to 0.
Here's the Desmos visualization you can explore yourself: https://www.desmos.com/calculator/tqkukhqjuu.
And our definitions:
How to offset liquidation risk
Hayes’ also outlines other risks.
One detail I didn't mention about perps above is the mechanism that keeps the prices of the perps itself in line with the asset they are tracking.
This is called the funding rate.
In practice, there are more longs seeking crypto exposure. Without a funding rate the value of the perp would track higher than the underlying asset (BTC).
So longs generally pay shorts.
This is what (potentially) makes the Nakamoto Dollar sustainable.
Hayes’ recommends using the funding rate income and putting it into a sinking fund that can be used to cover shortfalls due to liquidations or other reasons (custody issues with Bitcoin as well as the funding rate potentially turning negative in the future).
Hopefully this deep dive gives you more intuition of how perpetuals enable the creation of a synthetic dollar asset.
Now you should be able to go back and read the original post.
In follow-up essays I will explain how Ethena builds on these ideas.